Python 背包问题

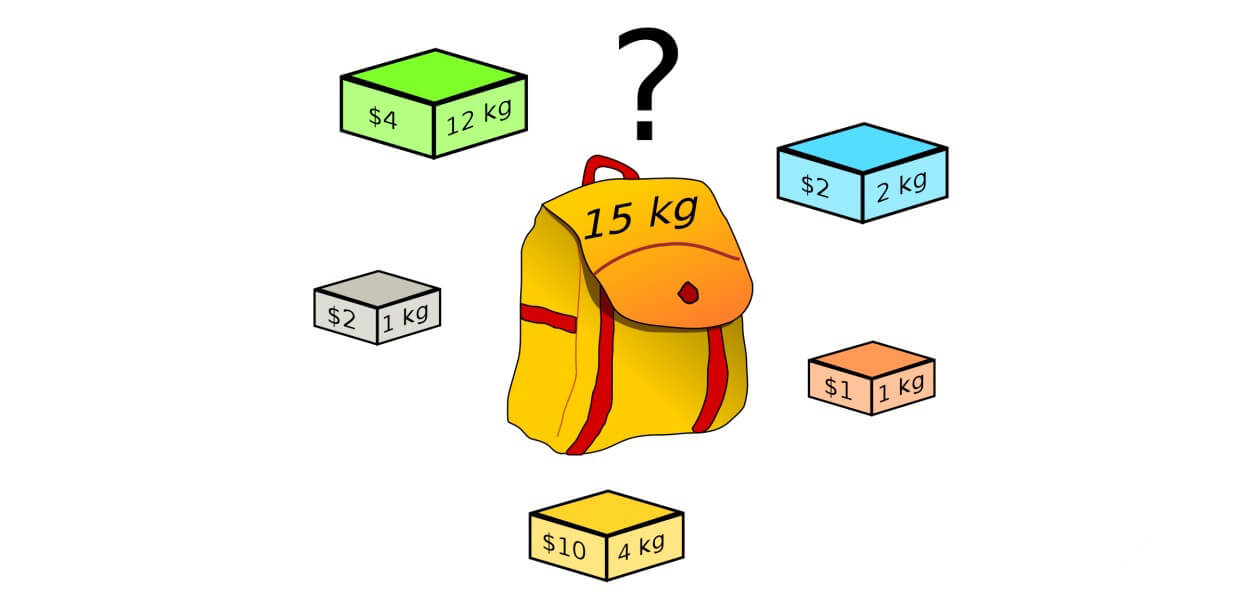
背包问题

背包问题（Knapsack Problem）是一类常见的组合优化问题。其问题描述为：给定一个固定大小、能够携重WW 的背包，以及一组有价值和重量的物品，找出一个最佳解决方案，使得装入背包的物品总重量不超过WW，且总价值最大。

背包问题

通常情况下，背包问题可以分为以下三类：

  • 0-1 背包问题：每种物品仅有一件，可以选择放或不放。
  • 完全背包问题：每种物品有无限件，可以选择放多少件或不放。
  • 多重背包问题：每种物品有nin_i 件，可以选择放多少件或不放。

本文将介绍如何使用 Python 解决以上三类背包问题。

0-1 背包问题

0-1 背包问题（0-1 Knapsack Problem）是最基础的背包问题。其问题描述为：给定一个固定大小、能够携重WW 的背包，以及NN 个价值、重量分别为viv_i、wiw_i 的物品，找出一个最佳解决方案，使得装入背包的物品总重量不超过WW，且总价值最大。

例

有一个容量为1010 的背包，现有44 个物品，其价值和重量分别为：

物品1234
价值1359
重量2347

求背包能装下的最大价值以及取得最大价值时的物品组合。

解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
N = 4  # 物品数量
W = 10  # 背包容量
v = [0, 1, 3, 5, 9]  # 物品价值
w = [0, 2, 3, 4, 7]  # 物品重量
dp = [[0] * (W + 1) for _ in range(N + 1)]  # dp[i][j] 表示前 i 个物品放入容量为 j 的背包的最大价值
flag = [
    [0] * (W + 1) for _ in range(N + 1)
]  # flag[i][j] 表示前 i 个物品放入容量为 j 的背包最大价值时装入物品的最大编号

# dp 求解最大价值并更新 flag
for i in range(1, N + 1):
    for j in range(1, W + 1):
        if j < w[i]:
            dp[i][j] = dp[i - 1][j]
        elif dp[i - 1][j] > dp[i - 1][j - w[i]] + v[i]:
            dp[i][j] = dp[i - 1][j]
            flag[i][j] = flag[i - 1][j]
        else:
            dp[i][j] = dp[i - 1][j - w[i]] + v[i]
            flag[i][j] = i - 1
ans = dp[N][W]

# 追踪解方案
sol = [0] * N
while flag[N][W] != 0:
    temp = flag[N][W]
    sol[temp] = 1
    W -= w[temp]
    N = temp - 1

# 输出结果
print(f"最大价值为：{ans}")
print(f"取得最大价值时的物品组合为：{sol}")

结果

1
2
最大价值为：12
取得最大价值时的物品组合为：[0, 1, 0, 1]

完全背包问题

完全背包问题（Unbounded Knapsack Problem）是背包问题的一种变种。其问题描述为：给定一个固定大小、能够携重WW 的背包，以及NN 个价值、重量分别为viv_i、wiw_i 的物品，每种物品有无限件，可以选择放多少件或不放，找出一个最佳解决方案，使得装入背包的物品总重量不超过WW，且总价值最大。

例

有一个容量为1515 的背包，现有44 个物品，其价值和重量分别为：

物品1234
价值1359
重量2347

求背包能装下的最大价值以及取得最大价值时的物品组合。

解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
N = 4  # 物品数量
W = 15  # 背包容量
v = [0, 1, 3, 5, 9]  # 物品价值
w = [0, 2, 3, 4, 7]  # 物品重量
dp = [[0] * (W + 1) for _ in range(N + 1)]  # dp[i][j] 表示前 i 个物品放入容量为 j 的背包的最大价值
flag = [
    [0] * (W + 1) for _ in range(N + 1)
]  # flag[i][j] 表示前 i 个物品放入容量为 j 的背包最大价值时装入物品的最大编号

# dp 求解最大价值并更新 flag
for i in range(1, N + 1):
    for j in range(1, W + 1):
        if j >= w[i]:
            if dp[i - 1][j] < dp[i][j - w[i]] + v[i]:
                dp[i][j] = dp[i][j - w[i]] + v[i]
                flag[i][j] = i
            else:
                dp[i][j] = dp[i - 1][j]
                flag[i][j] = flag[i - 1][j]
        else:
            dp[i][j] = dp[i - 1][j]
            flag[i][j] = flag[i - 1][j]
ans = dp[N][W]

# 追踪解方案
sol = [0] * N
while flag[N][W] != 0:
    N = flag[N][W]
    sol[N - 1] = 1
    W -= w[N]
    while flag[N][W] == N:
        W = W - w[N]
        sol[N - 1] += 1

# 输出结果
print(f"最大价值为：{ans}")
print(f"取得最大价值时的物品组合为：{sol}")

结果

1
2
最大价值为：19
取得最大价值时的物品组合为：[0, 0, 2, 1]

多重背包问题

多重背包问题（Bounded Knapsack Problem）是背包问题的一种变种。其问题描述为：给定一个固定大小、能够携重WW 的背包，以及NN 个价值、重量分别为viv_i、wiw_i 的物品，每种物品有nin_i 件，可以选择放多少件或不放，找出一个最佳解决方案，使得装入背包的物品总重量不超过WW，且总价值最大。

例

有一个容量为2525 的背包，现有44 个物品，其价值、重量、数量分别为：

物品1234
价值1359
重量2347
数量5432

求背包能装下的最大价值以及取得最大价值时的物品组合。

解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
N = 4  # 物品数量
W = 25  # 背包容量
v = [0, 1, 3, 5, 9]  # 物品价值
w = [0, 2, 3, 4, 7]  # 物品重量
n = [0, 5, 4, 3, 2]  # 物品数量
dp = [[0] * (W + 1) for _ in range(N + 1)]  # dp[i][j] 表示前 i 个物品放入容量为 j 的背包的最大价值
flag = [
    [0] * (W + 1) for _ in range(N + 1)
]  # flag[i][j] 表示前 i 个物品放入容量为 j 的背包最大价值时装入物品的最大编号

# dp 求解最大价值并更新 flag
for i in range(1, N + 1):
    for j in range(1, W + 1):
        for k in range(min(n[i], j // w[i]) + 1):
            if dp[i][j] < dp[i - 1][j - k * w[i]] + k * v[i]:
                dp[i][j] = dp[i - 1][j - k * w[i]] + k * v[i]
                flag[i][j] = k
ans = dp[N][W]

# 追踪解方案
sol = [0] * N
j = W
for i in range(N, 0, -1):
    sol[i - 1] = flag[i][j]
    j -= flag[i][j] * w[i]
# 输出结果
print(f"最大价值为：{ans}")
print(f"取得最大价值时的物品组合为：{sol}")

结果

1
2
最大价值为：31
取得最大价值时的物品组合为：[0, 1, 2, 2]